Case Study: Fraction Math

Case Study: Fraction Math

This topic presents a case study designed to bring together the concepts examined up to this point. The vehicle for the case study is a "fraction math" application, which allows the user (such as a grade school child, or parent of that child trying to help their kid with the homework) perform one of the four basic arithmetic operations (addition, subtraction, multiplication, or division) on a pair of fractional numbers.

The program will allow the user to choose one of the four operations (add, subtract, multiply, or divide). Text boxes will be presented for the user to enter in the two terms of the problem (the problem will be limited to two "terms", or items to be operated on). Each term can be either a fraction (for example, ), a mixed number (for example, 2 ), or a whole number (for example, 4). Therefore, each term will consist of three textboxes: one for the whole number portion of the problem (if any), one for the fraction numerator, and one for the fraction denominator.

After the user has entered the data for the problem and clicks the "Calculate" button, the program will display the result of the calculation. The result is expressed as a fraction, reduced to lowest terms.

The form also contains a "Clear" button, which allows a user to perform a new calculation, and an "Exit" button, which allows a user to exit the program. The form uses appropriate tabbing order and access keys.

In case you are a little rusty, here is a brief review of fraction math:

First, if there is a mixed number in the problem, convert this to a fraction by multiplying the integer portion of the number by the denominator of the fraction, then add the numerator to this result. This result becomes the new numerator, and the integer portion is discarded.

For example, 2 becomes .

Addition

After converting any mixed numbers to fractions, you must find a common denominator for both fractions. Adjust the numerators appropriately for the new denominators by multiplying the numerator by the same number you used to get the new denominator, add the numerators together and place that result over the common denominator, then convert the result back to a mixed number.

Sample problem:

2 + = ?

2 + = + = + = = 3

Subtraction

(Similar to addition.) After converting any mixed numbers to fractions, you must find a common denominator for both fractions. Adjust the numerators appropriately for the new denominators by multiplying the numerator by the same number you used to get the new denominator, subtract the numerators and place the difference over the common denominator, then convert the result back to a mixed number.

Sample problem:

2 - 1 = ?

2 - 1 = - = - = = 1

Multiplication

Convert any mixed numbers to fractions. Multiply the two numerators; that product becomes the new numerator. Multiply the two denominators; that product becomes the new denominator. Convert the final result back to a mixed number.

Sample problem:

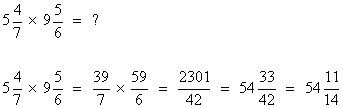
Division

(Similar to multiplication.) Convert any mixed numbers to fractions. Switch the numerator and the denominator of the second factor. Proceed as in multiplication.

Sample problem:

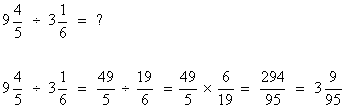
The programming solution consists of three modules – two form modules (a splash screen and the main form) and one standard module (contains one function procedure that could be used in any number of different projects).

Run-time screens are below, followed by an explanation of how the forms were built and a listing of the VB code.

When the user first runs Fraction Math, the following "splash screen" briefly appears:

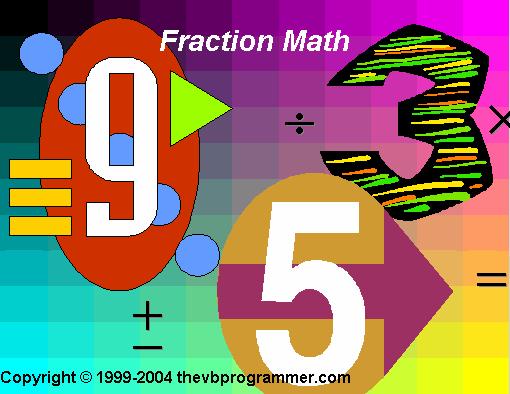
The main screen then appears, where the user can select which operation they wish to perform ("Add" is the default) and key in the numbers that make up the problem:

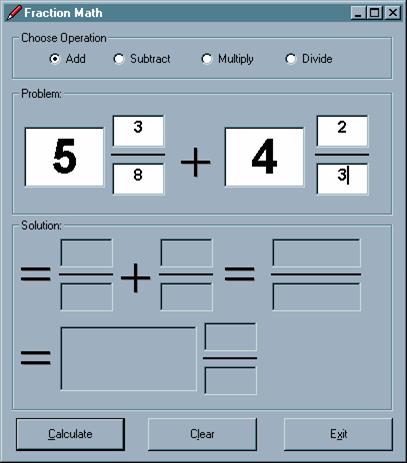
When the user clicks the Calculate button, the solution is displayed. Note that some of the intermediate results of the solution were displayed. This was a design choice; others might have

opted to just display the final result.

Designing Fraction Math

The following section describes how the Fraction Math application was created. You may wish to build this application as a tutorial. We will start with the design of the forms.

The Splash Screen

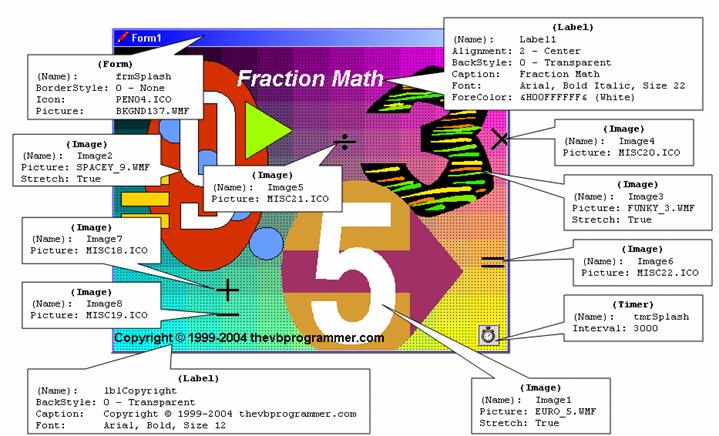
The admittedly garish splash screen is shown below, with callouts for each control used. The callouts indicate the names and property settings for each control as well as for the form itself.

The ".WMF" files were taken from a clip-art collection called "Art Explosion"; the four files used here (for the form background, the "big 3", "big 9", and "big 5") are included with the download for this project. The ".ICO" files are all from the Graphics collection that is included with Visual Studio/Visual Basic 6. The "PEN04.ICO" icon is from the "Writing" folder, all of the other icons are from the "Misc" folder.

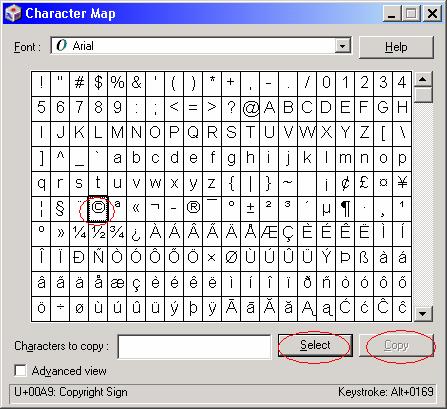
Note: To get the copyright symbol to display in the label at design-time, you need to use the Windows Character Map utility. On a Windows 2000 machine, you can get to it from the Start button, then Programs -> Accessories -> System Tools -> Character Map (if you are using a different OS, the path may be different).

When the Character Map utility comes up, first locate the desired character (the copyright symbol in this case), the click the Select button, which will enable the Copy button. Click the Copy button.

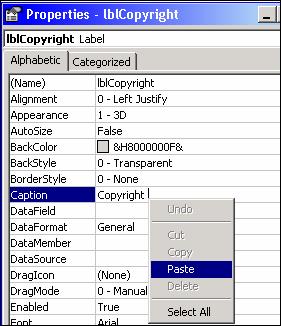
Back in your VB IDE, paste the symbol you just copied into the appropriate spot on the property sheet:

The Main Form

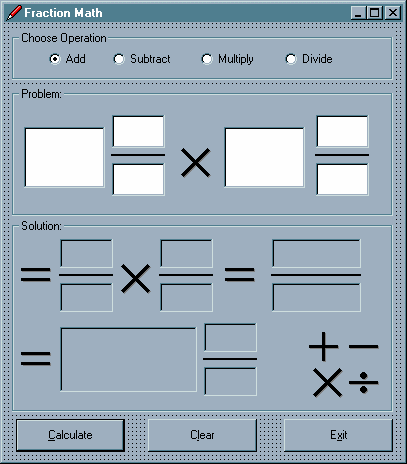
The main form for the Fraction Math application, as it looks at design-time, is shown below:

With the aid of screen-shots with callouts, the names and property settings for each control on the form, as well as for the form itself, will be shown in sections.

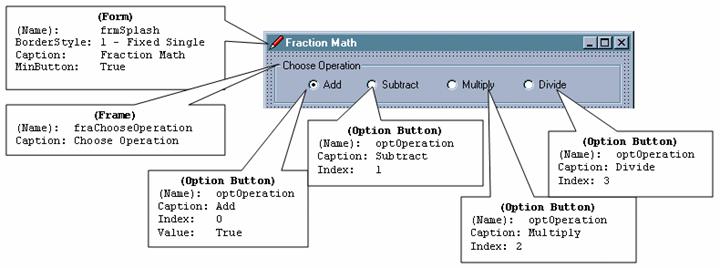
The first section of the form is shown below. Note that for the Form, the BorderStyle property was set to 1 – Fixed Single. This means that the user will not be able to resize the form. When you set the BorderStyle to 1 – Fixed Single, VB will automatically set the MinButton and MaxButton properties to False. However, since I want to allow the user to minimize the form, I set the MinButton property back to True.

In the "Choose Operation" frame (named "fraChooseOperation"), note that there is a control array of four option buttons, named "optOperation", indexed 0 to 3. Recall that option buttons work as a group, and only one can be "on " at a given time. Recall also that an option button group works within a "container" (such as a frame or the form itself).

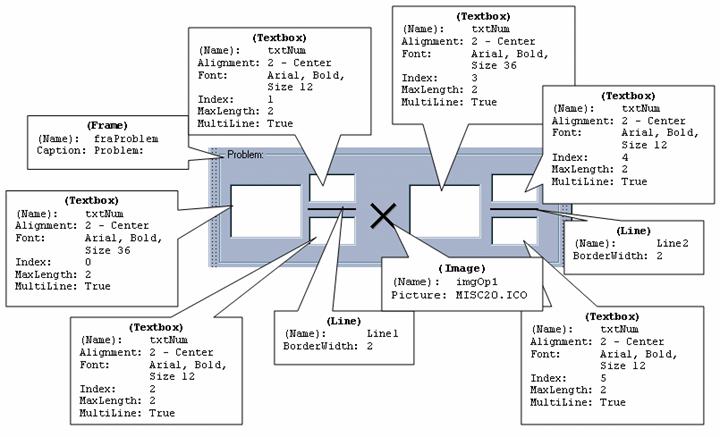
The next portion of the form shown is the "Problem:" frame, named "fraProblem". Inside this frame, there is a control array of six textboxes, named "txtNum", indexed 0 to 5, each with their MaxLength property set to 2 (we are limiting the input of the integer, numerator, and denominator portions of each term to a maximum value of 99). Note also that each textbox here has its MultiLine property set to true. That may seem odd, because the user will not be entering mutliple lines of text in these boxes. The reason that the MultiLine property is set to true is that we want the Alignment of the data entered into the boxes to be centered – and an anomoly of VB is that the Alignment property will only be "honored" if the MultiLine property is set to True. Otherwise, the text will always be aligned left regardless of the setting of the Alignment property.

The lines for the fractions are Line controls with the default VB names "Line1" and "Line2". The multiplication symbol in the middle is an Image control named "imgOp1"; at run-time, it will display a plus, minus, times, or division symbol depending on the option button selected above.

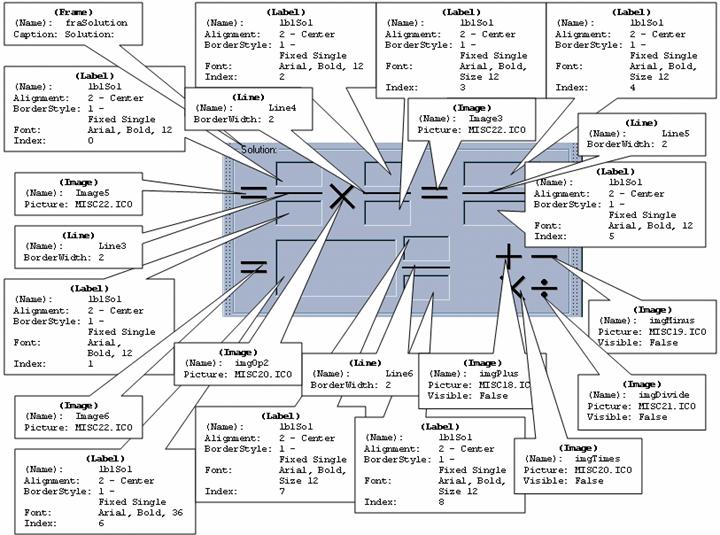
The next portion of the form shown is the "Solution:" frame, named "fraSolution". Inside this frame, there is a control array of nine labels, named "lblSol", indexed 0 to 8. These labels will display both the intermediate results of the calculation as well as the final solution. The lines for the fractions are Line controls with the default VB names "Line3", "Line4", "Line5", and "Line6". The multiplication symbol in the middle is an Image control named "imgOp2"; at run-time, it will display a plus, minus, times, or division symbol depending on the option button selected above. The "equal signs" are Image controls with default names ("Image3", "Image5", "Image6").

On the bottom right of the Solution frame, you see the four math symbols; these are Image controls named "imgPlus", "imgMinus", "imgTimes", and "imgDivide". The Visible property of these four image controls is set to False. This set of four images is used as an "image repository" for the symbols needed by the application. At run-time, depending on what option button is selected above, the Picture property of the appropriate hidden image will be assigned to the Picture property of the imgOp1 and imgOp2 controls. (This technique was discussed in a previous topic on images.)

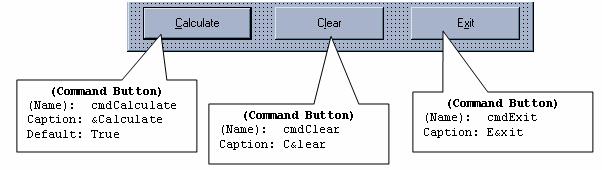
The bottom portion of the form contains three command buttons, named "cmdCalc", "cmdClear", and "cmdExit", each with appropriate access-key enabled Captions. Note that the Default property of the Calculate button is set to True. Recall that setting a command button's Default property to True allows that button's Click event code to be executed by pressing the Enter key.

Coding the Fraction Math Application

The heavily documented code for the application is presented below. This application uses a .BAS module in addition to the two forms discussed above. To add a module to your project, go to the Project menu of the IDE and choose Add Module:

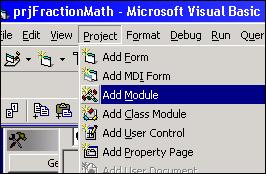
The Add Module dialog box appears, enabling you to add either a New or Existing module to your project. In this case, you would accept the default of New and click the Open button:

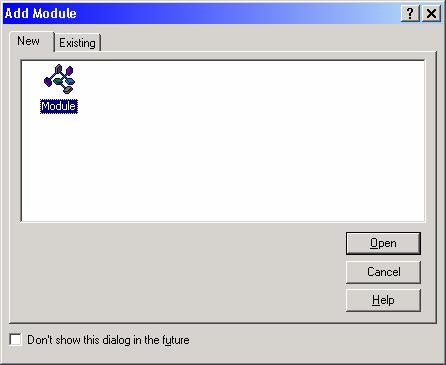
An empty code module window, with the default name "Module1", is then displayed:

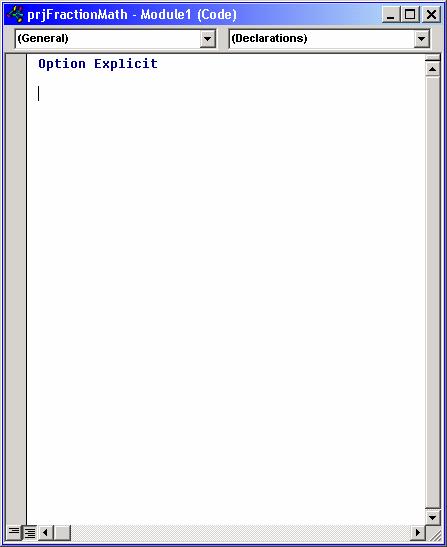
To rename the module, press F4 while the module window is open, which will bring up its property sheet. (A module has only one property, which is the Name.) Enter the new name in the property sheet. For this application, we are using the name "modCommon".

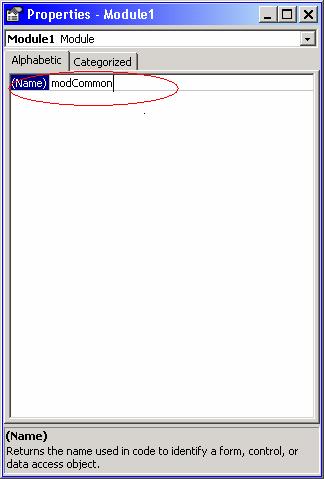
The code for modCommon is shown below. Generally, the code that is placed in a .BAS module consists of variables, constants, Subs, and Functions that are "Public", meaning the code is accessible all forms and modules within the application. In this case, the module contains a "CenterForm" routine, which is called by both forms to center themselves on the screen, as well as a "ValidKey" routine, which is used several times by the main form to filter out non-numeric keystrokes when entering the terms of the problem to be solved.

Code for modCommon:

Option Explicit

'------------------------------------------------------------------------

' Define key constant groups that can be used by any form or module in

' any project in which this module is included ...

'------------------------------------------------------------------------

Public Const gstrUPPER_ALPHA As String * 26 = "ABCDEFGHIJKLMNOPQRSTUVWXYZ"

Public Const gstrLOWER_ALPHA As String * 26 = "abcdefghijklmnopqrstuvwxyz"

Public Const gstrALPHABETIC As String * 52 = gstrUPPER_ALPHA & gstrLOWER_ALPHA

Public Const gstrNUMERIC_DIGITS As String * 10 = "0123456789"

'************************************************************************

Public Sub CenterForm(pobjForm As Form)

'************************************************************************

With pobjForm

.Top = (Screen.Height - .Height) / 2

.Left = (Screen.Width - .Width) / 2

End With

End Sub

'************************************************************************

'* *

Public Function ValidKey(pintKeyValue As Integer, _

pstrSearchString As String) As Integer

'* *

'* Common function to filter out keyboard characters passed to this *

'* function from KeyPress events. *

'* *

'* Typical call: *

'* KeyAscii = ValidKey(KeyAscii, gstrNUMERIC_DIGITS) *

'* *

'************************************************************************

If pintKeyValue < 32 _

Or InStr(pstrSearchString, Chr$(pintKeyValue)) > 0 Then

'Do nothing - i.e., accept the Backspace key and any key

' in the search string passed to this function ...

Else

'cancel (do not accept) any other key ...

pintKeyValue = 0

End If

ValidKey = pintKeyValue

End Function

The code for the forms follows.

Code for frmSplash:

Option Explicit

Private Sub Form_Load()

CenterForm Me

End Sub

Private Sub tmrSplash_Timer()

tmrSplash.Enabled = False

frmMain.Show

Unload Me

End Sub

Code for frmMain:

Option Explicit

'***************************************************************************

' Module-Level (Form-Level) Variable Declarations *

'***************************************************************************

Private mblnFormActivated As Boolean

Private mintNewFocus As Integer

Private mstrErrorMsg As String

'***************************************************************************

' Form Event Procedures *

'***************************************************************************

'----------------------------------------------------------------------------

Private Sub Form_Activate()

'----------------------------------------------------------------------------

' Initialization code ...

If mblnFormActivated Then

' We only want to do this event once, so if we get here again

' (for example, the user starts this program, does something else

' in Windows, and then comes back), leave this sub ...

Exit Sub

End If

' Center the form on the screen using the programmer-defined CenterForm

' sub (located in this project's "BAS" module) ...

CenterForm Me

' Invoke the "operation" option button Click event, passing it a zero,

' indicating the "Add" operation (as if the user clicked the "Add"

' option button). This is a way of providing a default operation to the user ...

optOperation_Click 0

mblnFormActivated = True

End Sub

'***************************************************************************

' Option Button Event Procedures *

'***************************************************************************

'----------------------------------------------------------------------------

Private Sub optOperation_Click(Index As Integer)

'----------------------------------------------------------------------------

' When the user clicks an "operation" option button, put the appropriate

' symbols in the "Problem" and "Solution" frames. This is done by copying

' an "invisible" addition, subtraction, multiplication, or division image

' from its "hiding place" on the form to the image controls in the Problem

' and Solution frames ...

Select Case Index

Case 0

imgOp1.Picture = imgPlus.Picture

imgOp2.Picture = imgPlus.Picture

Case 1

imgOp1.Picture = imgMinus.Picture

imgOp2.Picture = imgMinus.Picture

Case 2

imgOp1.Picture = imgTimes.Picture

imgOp2.Picture = imgTimes.Picture

Case 3

imgOp1.Picture = imgDivide.Picture

imgOp2.Picture = imgTimes.Picture

End Select

' Set focus to the first textbox ...

txtNum(0).SetFocus

End Sub

'******************************************************************************

'* Textbox Event Procedures *

'* *

'* The three event procedures (GotFocus, KeyPress, and Change) are all *

'* shared among the 6 members of the txtNum control array (indexed 0 to 5). *

'* *

'* The GotFocus event contains the code to highlight the number in the *

'* textbox when the user moves focus to it. *

'* *

'* The KeyPress event invokes the programmer-defined ValidKey function *

'* (found the "BAS" module of this project) to ensure only digits are *

'* entered in the field. *

'* *

'* The Change event is coded to implement an "AutoTab" feature. When the *

'* user enters the maximum number of digits for each portion of the *

'* problem, they are automatically positioned on the next enterable control. *

'* *

'******************************************************************************

'----------------------------------------------------------------------------

Private Sub txtNum_GotFocus(Index As Integer)

'----------------------------------------------------------------------------

With txtNum(Index)

.SelStart = 0

.SelLength = Len(.Text)

End With

End Sub

'----------------------------------------------------------------------------

Private Sub txtNum_KeyPress(Index As Integer, KeyAscii As Integer)

'----------------------------------------------------------------------------

KeyAscii = ValidKey(KeyAscii, gstrNUMERIC_DIGITS)

End Sub

'----------------------------------------------------------------------------

Private Sub txtNum_Change(Index As Integer)

'----------------------------------------------------------------------------

With txtNum(Index)

If Len(.Text) = .MaxLength Then

If Index < 5 Then

txtNum(Index + 1).SetFocus

Else

cmdCalc.SetFocus

End If

End With

End Sub

'***************************************************************************

' Command Button Event Procedures *

'***************************************************************************

'----------------------------------------------------------------------------

Private Sub cmdCalc_Click()

' This event contains the code to solve the fraction math problem entered

' by the user and present the solution to the user. To get here, the user would

' have entered the numbers in the "Problem" frame's textboxes and clicked the

' "Calculate" button.

' The comments will document a sample problem. If the user put in 5 3/8 +

' 4 2/3, this routine will do the work to come up with a solution of 10 1/24.

'----------------------------------------------------------------------------

Dim lngNum(0 To 5) As Long 'Array of longs to store the numbers the

'user has entered in the Problem frame textboxes

Dim lngSol(0 To 8) As Long 'Array of longs containing the numbers comprising

'the solution to the problem

Dim lngCommDenom As Long

Dim lngTemp As Long

Dim intX As Integer

Dim intReducer As Integer

' First, do some error-checking with the programmer-defined function

' DataEntryError, which will return True if there is a problem and

' False if not. If there is an error, display the corresponding message,

' set focus to the offending textbox, and get out ...

If DataEntryError Then

MsgBox mstrErrorMsg, _

vbExclamation, _

"Fraction Math"

txtNum(mintNewFocus).SetFocus

Exit Sub

End If

' Load the lngNum array to hold the "Problem" numbers from the txtNum textboxes.

' Using our sample problem, after the completion of this loop, the contents of

' the lngNum array will be:

' (0) (1) (2) (3) (4) (5)

' --- --- --- --- --- ---

' 5 3 8 4 2 3

For intX = 0 To 5

lngNum(intX) = Val(txtNum(intX).Text)

' If either the numerator or the denominator of either the first or second

' number of the problem is zero, set them both to zero and clear those

' textboxes ...

If lngNum(1) = 0 Or lngNum(2) = 0 Then

lngNum(1) = 0

lngNum(2) = 0

txtNum(1).Text = ""

txtNum(2).Text = ""

End If

If lngNum(4) = 0 Or lngNum(5) = 0 Then

lngNum(4) = 0

lngNum(5) = 0

txtNum(4).Text = ""

txtNum(5).Text = ""

End If

' Convert mixed numbers to fractions. At this point we start to populate

' elements of the lngSol array. After the following section of code is

' complete, the contents of the lngSol array will be populated as follows:

' (0) (1) (2) (3) (4) (5) (6) (7) (8)

' --- --- --- --- --- --- --- --- ---

' 43 8 14 3

If lngNum(1) = 0 And lngNum(2) = 0 Then

lngSol(0) = lngNum(0)

lngSol(1) = 1

Else

lngSol(0) = (lngNum(0) * lngNum(2)) + lngNum(1)

lngSol(1) = txtNum(2).Text

End If

If lngNum(4) = 0 And lngNum(5) = 0 Then

lngSol(2) = lngNum(3)

lngSol(3) = 1

Else

lngSol(2) = (lngNum(3) * lngNum(5)) + lngNum(4)

lngSol(3) = lngNum(5)

End If

' If we are doing addition (as we are in the case of the sample problem) or

' subtraction, we must find the common denominator and adjust elements in

' the solution array (lngSol) accordingly. If we are doing division, switch

' the numerator and denominator of the second number so that it can be

' performed as multiplication. If we are doing multiplication, nothing

' special need be done at this point.

If optOperation(0).Value _

Or optOperation(1).Value Then

' For an addition or subtraction operation, find the common denominator

' and adjust elements in the solution array (lngSol) accordingly ...

' In our sample problem, the common denominator will be 24 (8 * 3):

lngCommDenom = lngSol(1) * lngSol(3)

' As the next four lines execute, the contents of the lngSol array

' will be populated as follows:

' (0) (1) (2) (3) (4) (5) (6) (7) (8)

' --- --- --- --- --- --- --- --- ---

lngSol(0) = lngSol(0) * lngSol(3) ' 129 8 14 3

lngSol(2) = lngSol(2) * lngSol(1) ' 129 8 112 3

lngSol(1) = lngCommDenom ' 129 24 112 3

lngSol(3) = lngCommDenom ' 129 24 112 24

ElseIf optOperation(3).Value Then

' Operation is division, so switch the numerator

' and denominator of the second number ...

lngTemp = lngSol(2)

lngSol(2) = lngSol(3)

lngSol(3) = lngTemp

End If

' The code in the Select Case structure below will populate elements (4) and

' (5) of the lngSol solution array, which will contain the numerator and

' denominator of the "raw" (non-reduced) solution ...

Select Case True

Case optOperation(0).Value

' For addition, add the numerators of the first and second numbers

' and place it over the common denominator.

' For our sample problem, after the two statements below execute,

' the contents of the lngSol array will be populated as follows:

' (0) (1) (2) (3) (4) (5) (6) (7) (8)

' --- --- --- --- --- --- --- --- ---

' 129 24 112 24 241 24

lngSol(4) = lngSol(0) + lngSol(2)

lngSol(5) = lngCommDenom

Case optOperation(1).Value

' For subtraction, subtract the numerators of the first and second

' numbers and place it over the common denominator ...

lngSol(4) = lngSol(0) - lngSol(2)

lngSol(5) = lngCommDenom

Case Else

' For a mulitplication problem, or a division probelm that was

' converted to multiplication in a previous step, multiply the

' numerators and denominators of the first and second numbers

' by each other ...

lngSol(4) = lngSol(0) * lngSol(2)

lngSol(5) = lngSol(1) * lngSol(3)

End Select

' Now, we must convert the "raw" result (numerator residing in lngSol(4),

' denominator residing in lngSol(5)) back to a mixed number. The three

' statements below will accomplish this, placing the integer portion of

' the mixed number in element (6) and the numerator and denominator of

' the mixed number in elements (7) and (8), respectively.

' For our sample problem, after the two statements below execute,

' the contents of the lngSol array will be populated as follows:

' (0) (1) (2) (3) (4) (5) (6) (7) (8)

' --- --- --- --- --- --- --- --- ---

' 129 24 112 24 241 24 10 1 24

lngSol(6) = lngSol(4) \ lngSol(5) ' Get the quotient

lngSol(7) = lngSol(4) Mod lngSol(5) ' Get the remainder

lngSol(8) = lngSol(5) ' Common denominator

' The following code serves to reduce (if necessary) the fractional

' protion of the final, mixed number result. In the case of the sample

' problem, the code will determine that reducing is not necessary in

' this particular case.

If lngSol(7) <> 0 Then

' Reduce the fractional portion of the final result by checking

' for a number that will divide evenly into both the numerator

' and the denominator. Do this by looping thru a set of values

' backwards, staring with the the value of the numerator, and working

' down toward a minimum of 2 ...

For intReducer = lngSol(7) To 2 Step -1

If (lngSol(7) Mod intReducer = 0) _

And (lngSol(8) Mod intReducer = 0) Then

' We've found a number that divides evenly into both

' the numerator and the denominator of the final answer,

' so divide and get out ...

lngSol(7) = lngSol(7) \ intReducer

lngSol(8) = lngSol(8) \ intReducer

Exit For

End If

' Display the solution (copy the values from the lngSol array into

' corresponding elements of the lblSol control array on the form ...

For intX = 0 To 8

lblSol(intX).Caption = lngSol(intX)

' Zero-suppress if necessary ...

If lngSol(6) = 0 And lngSol(7) = 0 Then

lblSol(6).Caption = "0'"

lblSol(7).Caption = ""

lblSol(8).Caption = ""

Else

If lngSol(6) = 0 Then

lblSol(6).Caption = ""

End If

If lngSol(7) = 0 Then

lblSol(7).Caption = ""

lblSol(8).Caption = ""

End If

' Set the form such that the user can't enter in a problem while

' the solution is displayed. (They can either hit the Clear button

' or Exit.)

SetFormState False, vbButtonFace

End Sub

'----------------------------------------------------------------------------

Private Sub cmdClear_Click()

' The Clear button prepares the form so that the user can enter a new

' problem by enabling the appropriate controls and clearing the txtNum

' and lblSol arrays.

'----------------------------------------------------------------------------

Dim intX As Integer

SetFormState True, vbWhite

For intX = 0 To 5

txtNum(intX).Text = ""

For intX = 0 To 8

lblSol(intX).Caption = ""

txtNum(0).SetFocus

End Sub

'----------------------------------------------------------------------------

Private Sub cmdExit_Click()

'----------------------------------------------------------------------------

End

End Sub

'----------------------------------------------------------------------------

Private Sub SetFormState(pblnEnabledValue As Boolean, _

plngBackColor As Long)

' This routine enables/disables controls on the form depending upon the

' state of the application: i.e., the user is either entering the data

' for the math problem, or is looking at the result.

'----------------------------------------------------------------------------

Dim intX As Integer

fraChooseOperation.Enabled = pblnEnabledValue

For intX = 0 To 3

optOperation(intX).Enabled = pblnEnabledValue

fraProblem.Enabled = pblnEnabledValue

For intX = 0 To 5

txtNum(intX).BackColor = plngBackColor

cmdCalc.Enabled = pblnEnabledValue

End Sub

'----------------------------------------------------------------------------

Private Function DataEntryError() As Boolean

' This routine is called by the "calc" procedure to make sure we have

' have good numbers before trying to solve the math problem. If any

' one of a number of data entry errors is encountered, an error message

' is set, we decide what textbox should get the focus, we set the return

' value of this function to True, and get out. The calc procedure will test

' the return value of this function and if True, will display the error

' message and set the focus appropriately.

'----------------------------------------------------------------------------

If txtNum(1).Text = "" And txtNum(2).Text <> "" Then

mstrErrorMsg = "The numerator of the first value is missing."

mintNewFocus = 1

DataEntryError = True

Exit Function

End If

If txtNum(2).Text = "" And txtNum(1).Text <> "" Then

mstrErrorMsg = "The denominator of the first value is missing."

mintNewFocus = 2

DataEntryError = True

Exit Function

End If

If txtNum(4).Text = "" And txtNum(5).Text <> "" Then

mstrErrorMsg = "The numerator of the second value is missing."

mintNewFocus = 4

DataEntryError = True

Exit Function

End If

If txtNum(5).Text = "" And txtNum(4).Text <> "" Then

mstrErrorMsg = "The denominator of the second value is missing."

mintNewFocus = 5

DataEntryError = True

Exit Function

End If

If optOperation(3).Value = True Then

If Val(txtNum(3).Text) = 0 And Val(txtNum(4)) = 0 Then

mstrErrorMsg = "Second value cannot be zero for division."

mintNewFocus = 3

DataEntryError = True

Exit Function

End If

DataEntryError = False

End Function

Download the VB project code for the example above here.